Un cerc poate fi transformat într-un pătrat folosind această formulă kirigami | Știri MIT

Kirigami duce cărțile pop-up la un nivel cu totul nou. Meșteșugurile de hârtie japoneze implică tăierea modelelor în hârtie pentru a transforma o foaie de hârtie bidimensională într-o structură tridimensională complicată atunci când este pliată parțial. În mâinile unui artist, kirigami poate produce replici remarcabil de detaliate și delicate ale structurilor din natură, arhitectură și multe altele.

Oamenii de știință și inginerii s-au inspirat, de asemenea, din kirigami, aplicând principii de la tăierea hârtiei până la proiectarea de prinderi robotizate, electronice extensibile, panouri de recoltare a apei și alte materiale și dispozitive care schimbă forma. În cea mai mare parte, aceste invenții sunt produse de design de la zero. Nu exista un plan pentru ingineri care să specifice modelul de tăieturi care să transforme materialul de la o formă dorită la alta – adică până acum.

A Studiu nou în Științe computaționale ale naturii Prezintă o strategie algoritmică generală care poate rezolva orice transformare 2D inspirată de kirigami. Metoda poate fi utilizată pentru a determina unghiul și lungimea tăierilor care trebuie făcute, astfel încât foaia să se poată transforma de la o formă dorită la alta atunci când este deschisă și împinsă împreună, ca o bandă complexă expandabilă.

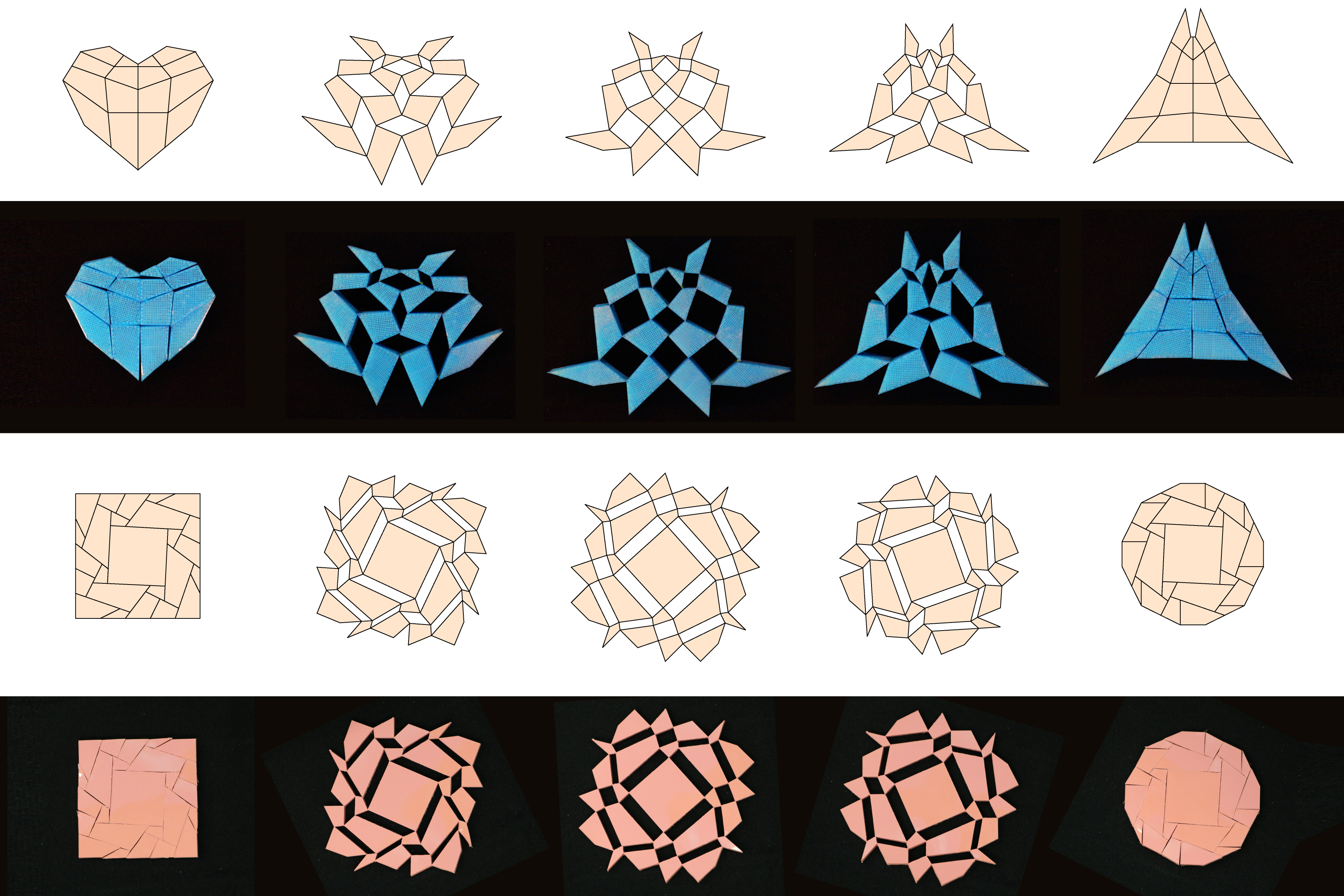
Cu noua lor metodă, cercetătorii au proiectat și construit o serie de structuri kirigami 2D transformabile, inclusiv un cerc care se transformă într-un pătrat și un triunghi care se transformă într-o inimă.

„Oamenii au vorbit despre pătrat și cerc ca fiind una dintre problemele imposibile în matematică: nu poți transforma una în alta”, spune Gary Choi, profesor postdoctoral și instructor de matematică aplicată la MIT. „Dar cu kirigami, putem de fapt transforma o formă pătrată într-o formă de cerc.”

Pentru ingineri, noua metodă ar putea fi folosită pentru a rezolva diverse probleme de proiectare, cum ar fi modul de proiectare a unui robot pentru a se transforma dintr-o formă în alta pentru a îndeplini o anumită sarcină sau a naviga în anumite spații. Există, de asemenea, potențialul de a proiecta materiale eficiente, de exemplu ca acoperiri inteligente pentru clădiri și case.

„Una dintre primele aplicații la care ne-am gândit a fost pentru fațadele clădirilor”, spune Caitlin Baker, profesor asistent de inginerie mecanică la MIT. „Acest lucru ne-ar putea ajuta să facem fețe mari, asemănătoare cu kirigami, care își pot schimba forma pentru a controla lumina soarelui și radiațiile ultraviolete și pentru a se adapta la mediul lor”.

Baker și Choi sunt coautorii noului studiu, împreună cu Levi Dowdy, cercetător cantitativ la Optiver, și L. Mahadevan, profesor la Universitatea Harvard.

spatiu intre

Studiul a luat naștere din munca anterioară a echipei atât pe kirigami, cât și pe origami – arta japoneză a plierii hârtiei.

„Am descoperit că există o mulțime de conexiuni matematice în kirigami și origami”, spune Choi. „Așa că am vrut să venim cu o formulă matematică care ar putea ajuta oamenii să proiecteze o mare varietate de modele.”

În 2019, echipa a conceput o metodă de îmbunătățire pentru kirigami pentru a găsi modelul de tăieturi necesar pentru a transforma o formă în alta. Dar Choi spune că abordarea a fost foarte intensivă din punct de vedere computațional și a durat mult timp pentru a obține un model ideal pentru a realiza o schimbare specifică.

În 2021, cercetătorii s-au confruntat cu o problemă similară cu origami și au descoperit că, printr-o lentilă ușor diferită, au reușit să obțină o strategie mai eficientă. În loc să traseze un model de pliuri individuale (similar cu bucățile individuale de kirigami), echipa sa concentrat pe creșterea unui model dintr-o sămânță simplă pliată. Lucrând placă cu placă și stabilind relații între plăci, cum ar fi modul în care o placă s-ar mișca dacă o placă adiacentă ar fi pliată, au reușit să obțină un algoritm relativ eficient pentru planificarea designului oricărei structuri origami.

Echipa s-a întrebat dacă o abordare similară ar putea fi aplicată pentru kirigami. În kirigami tradițional, odată ce tăierea este făcută într-o foaie de hârtie, foaia poate fi parțial pliată, astfel încât spațiile goale rezultate să creeze o structură tridimensională. La fel ca panourile dintre faldurile origami, spațiile goale dintre tăieturi și relația dintre ele ar putea oferi o versiune mai eficientă a designului kirigami? Această întrebare este impulsul pentru noul studiu al echipei.

Legături de matematică

Studiul se concentrează pe transformările kirigami bidimensionale. Cercetătorii au considerat un design kirigami generic constând dintr-un mozaic de plăci patrulatere interconectate, fiecare tăiată în unghiuri și dimensiuni diferite. Mozaicul conceptual începe ca o singură formă și poate fi separat și împins împreună pentru a forma o formă complet nouă. Provocarea a fost de a descrie modul în care o formă se poate transforma în alta, pe baza spațiilor goale dintre plăci și modul în care spațiile se schimbă atunci când plăcile sunt trase și împinse înapoi împreună.

„Dacă plăcile în sine sunt solide și imuabile, spațiile goale dintre ele sunt o oportunitate de mișcare”, spune Baker.

Echipa a analizat mai întâi cea mai simplă reprezentare a spațiului gol, ca un romb sau ceea ce ei numesc o „legătură cu patru bare”. Fiecare parte a rombului reprezintă o bandă sau marginea unei plăci solide. Fiecare colț al rombului reprezintă o legătură sau balama care leagă pătratele. Variind lungimea și unghiul marginilor romburilor, echipa poate studia modul în care spațiul gol se schimbă între schimbări.

Studiind grupuri mai mari de legături cu patru bare, echipa a determinat relațiile dintre unghiul și lungimea tijelor, forma golurilor individuale și forma ansamblului general. Ei au transformat aceste relații într-o formulă generală și au descoperit că ar putea determina eficient modelul de tăiere – inclusiv unghiul și lungimea – care ar fi necesar pentru a converti o foaie de hârtie bidimensională de la o formă dorită la alta.

„Fără un astfel de instrument, aș putea forța brută această problemă în Matlab, sau ghicesc și verific, dar ar dura foarte mult timp pentru a obține ceva care s-ar putea transforma dintr-un cerc într-un pătrat”, spune Baker.

În simulări, echipa a descoperit că formula ar putea găsi de fapt un model de plăci care transforma un mozaic în formă de cerc într-un pătrat, precum și aproape orice formă în orice altă formă dorită.

Mergând mai departe, echipa a dezvoltat două metode de producție pentru a-și realiza efectiv modelele de formule. Curând și-au dat seama că principala provocare în realizarea mozaicurilor transferabile a fost găsirea materialului potrivit care să acționeze ca balamale de îmbinare a plăcilor. Îmbinările trebuie să fie puternice și ușor de îndoit.

„M-am gândit: Ce este atât de puternic la tensiune, rezistent la rupere, dar poate avea o rază de curbură zero, aproape ca o balama de precizie?” spune Baker. Și se pare că răspunsul este țesut.

Echipa a folosit două metode – imprimarea 3D și turnarea sub presiune – pentru a încorpora mici benzi de țesătură în plăci de plastic pe patru fețe, într-un mod care leagă strâns plăcile, permițându-le în același timp să se sprijine una de cealaltă. Folosind aceste două metode, echipa a realizat un mozaic de cercuri care s-au transformat în pătrate, precum și un mozaic de triunghiuri simple care s-au transformat în forme de inimă mai complexe.

„Putem merge în practic în orice formă bidimensională”, spune Choi. „Acest lucru este sigur, folosind formula noastră matematică. Acum căutăm să extindem acest lucru în kirigami 3D.”